Amazon Q CLIでゲームを作ってみた
最近はClaude CodeやGemini CLIなど、従来のレベルを超えた？AIエージェントが登場しており、驚かされます。
何か試そう・・・と考えていた時に、以下キャンペーンも気になったので、Amazon Q CLIを使ったゲーム作りに挑戦してみました。
aws.amazon.com
PCにWSL, Ubuntu環境が既に入っていたため、試してみようと思ってから5分後にはAmazon Q CLIが動作し、さらに5分後にはゲームが完成。まさに恐るべきスピードの時代です。
目次
🖥️開発環境
このプロジェクトは以下の環境で開発・動作確認を行いました。
- OS: Windows 11 Home
- 開発環境: WSL2（Windows Subsystem for Linux）
- Linuxディストリビューション: Ubuntu 24.04.1 LTS（Codename: noble）
- Pythonバージョン: 3.12.3
- パッケージ管理: pip（仮想環境には `venv` を使用）
構成について
できたプログラムはシンプルな構成で、以下の通りです。
構成詳細
│─ run_game.sh │─ rvertical_shooter.py
コードはGitHubにも保存をしています。
github.com
Amazon Q CLIでゲームを作ってみる
Amazon Q CLIの導入
イベント公式のページから飛べる以下ページの通りなのですが・・まとめておきます。
community.aws
WSL, Ubuntuインストール(既にインストール済みのため、省略)
Amazon Qインストール
Ubuntu（WSL2）上のターミナルで、以下のコマンドを入力します： sudo apt install unzip curl --proto '=https' --tlsv1.2 -sSf https://desktop-release.codewhisperer.us-east-1.amazonaws.com/latest/q-x86_64-linux-musl.zip -o q.zip ./install.sh --force
これだけで、使えてしまいます。
Amazon Q CLIを動かしてみた
以下コマンドでAmazon Qが立ち上がります。
Ubuntu（WSL2）上のターミナルで、以下のコマンドを入力します： q
今回は、縦型のシューティングゲームを作ってもらおうということで、頼んでみました。
その後、どんどん自身でファイル類を作成して、コードを作ってくれます。
という感じで、ファイル類を作成して、その説明を加えて終了。依頼をしてから2~3分くらいで完了しました。
作ったゲームを動かしてみる
ちゃんと遊べるゲームができていました。
まとめ
環境構築などで少し時間がかかるだろうな、と思っていたのですが、今回はあっという間にできてしまってびっくりしました。WSL環境との相性もよくて、サクッと動くのも好印象。
これからもいろんな使い方を試してみたくなりました！
最近は仕事でもクラウド関連に触れることが多く、気づけば1年ほどブログをお休みしていました。
でも、やっぱり「おもしろい！」と思えたことを言葉にして残すのは楽しいですね。
業務でのLLM活用検討とプロンプティングの難しさ
業務でのLLM利活用を想定した取り組みの中で、プロンプティングの難しさに直面したので、試したことをまとめます。
目次
業務でのLLM利活用について
LLMで業務効率化が図れないかなと考える中(以下リスト)で、色々なサービスベンダーが既に出している(汎用性が高い)領域も多くあったので、実際の現場に近い担当者が独自で開発した方が良いものってないかなという視点で、開発ターゲットを選定してみました。
| 活用案 | 活用するまでのハードル | 理由 |
| 社内ナレッジを活用したChatBot | 低~高 | Google Vertex AI等 複数ベンダーが提供しているサービスがあり、サービスをそのまま使える為 ハードルが低いが、求められる出力レベルによってはハードル高い |
| 議事録の自動作成 | 低い | 複数ベンダーが提供しているサービスがあり、サービスをそのまま使える為 ハードルが低い |
| ソースコードの理解/作成支援 | 低い | 複数ベンダーが提供しているサービスがあり、サービスをそのまま使える為 ハードルが低い |
| 書類の自動チェック | 高い | 複数ベンダーが提供しているサービスがあるが、社内ナレッジ向けにカスタマイズが必要であり、ハードルが高い |
この中で、社内ナレッジを活用したChatBot作成事例や作成フローの紹介は色々なページで紹介があるので、書類の自動チェックをLLMに実施させる方法は事例がなかなか見当たらなかったので、トライしました。
「書類の自動チェックする」システムの作成
現状、書類（開発書類）は抜け漏れなく記載されているかどうかを人がチェックしていますが、このチェックを自動化して効率化を図りたいと考えました。
| 現状 | 望むべき未来 | ソリューション案 |
| 人が一つ一つ書類をチェック | 自動で書類がチェックされてその結果が返ってくる | LLMを活用する |
書類が正しく書けているかどうかは、「文章の正しさ」や「一貫性があるかどうか」が関係するため、LLMを使うのが適切と考えました。
とりあえずやってみる
結論から言うと、とりあえず何も考えずに以下のようなプロンプトを与えてチェックをしてみたのですが、うまくいかないことが非常に多くありました。
使用するモデルと実施方法
Gemini Pro-1.5を使おうか迷いましたが、試した時点で一番最新だったGPT-4oを使いました。APIとしての使い方ではなく、アプリでの使い方のため、TemperatureやTop_pなどの設定はできません。続けて会話をすると履歴の中に答えが混ざってしまうので、1回聞くごとに違う会話ウィンドウで聞くということを繰り返しています。（面倒ですが、GPT-4oを試したかった）
用意したデータ
Google Geminiに架空のプロジェクト書類とチェックリストを作成してもらい、チェックリストに対してNGが出るような文章も作成してもらいました。
作成したプロジェクト書類
要件仕様書 プロジェクト概要 プロジェクト名: 新規Webアプリケーション開発 プロジェクト番号: DEV24-01 目的: 中小企業向けにカスタマイズ可能な在庫管理システムを提供する。 期間: 2023年6月1日から2023年12月31日 機能要件 在庫登録機能: 商品の追加、編集、削除ができる。商品ごとにカテゴリ分けが可能。 在庫検索機能: 商品名、カテゴリ、価格帯など複数の条件で検索可能。 在庫報告機能: 指定期間内の在庫動向を報告書として出力。在庫過多や不足があった場合のアラート機能。 ユーザー管理機能: ユーザー登録、ログイン、権限管理。 非機能要件 パフォーマンス: 画面の応答時間は2秒以内。 セキュリティ: GDPRに準拠したデータ保護。 スケーラビリティ: 最大1000ユーザー同時アクセスをサポート。 利害関係者 エンドユーザー: 在庫管理を行う中小企業の従業員。 開発チーム: ソフトウェアエンジニア、プロジェクトマネージャー。 クライアント: XYZ株式会社。 リスク評価 - リスク1: プロジェクトの遅延 - 対策: 定期的な進捗確認と問題の早期発見 - リスク2: セキュリティ脆弱性 - 対策: 定期的なセキュリティテストと脆弱性の迅速な修正 - リスク3: ユーザーの要件変更 - 対策: 変更管理プロセスを設け、変更要求を適切に評価・対応 承認プロセス - ドキュメントレビュー: プロジェクトマネージャー、クライアント代表者、主要な技術者がレビューを行う。 - 承認手順: レビュー完了後、各担当者が承認のサインを行う。 - 文書管理: 全てのドキュメントはプロジェクト管理システムに保存され、変更履歴を追跡可能にする。 変更管理プロセス - 変更要求の提出: 利害関係者は公式な変更要求書を提出する。 - 変更評価: 提出された変更要求は、技術的・スケジュール的・コスト的な影響を評価される。 - 変更承認: 評価結果に基づき、承認または却下が行われる。 - 変更実施: 承認された変更は、プロジェクト計画に反映され、実施される。 ワークブレイクダウン構造(WBS) 1. プロジェクト管理: 2023年6月1日 - 2023年6月14日 - 計画策定: 2023年6月1日 - 2023年6月7日 - リスク管理: 2023年6月8日 - 2023年6月14日 2. 要件定義: 2023年6月15日 - 2023年7月5日 - 利害関係者インタビュー: 2023年6月15日 - 2023年6月21日 - 要件ワークショップ: 2023年6月22日 - 2023年6月28日 - 要件文書化: 2023年6月29日 - 2023年7月5日 3. 設計: 2023年7月6日 - 2023年7月20日 - アーキテクチャ設計: 2023年7月6日 - 2023年7月12日 - データベース設計: 2023年7月13日 - 2023年7月20日 4. 開発: 2023年7月21日 - 2023年9月15日 - フロントエンド開発: 2023年7月21日 - 2023年8月10日 - バックエンド開発: 2023年8月11日 - 2023年9月15日 5. テスト: 2023年9月16日 - 2023年10月15日 - 単体テスト: 2023年9月16日 - 2023年9月30日 - 結合テスト: 2023年10月1日 - 2023年10月15日 6. デプロイメント: 2023年10月16日 - 2023年11月15日 - デプロイ計画: 2023年10月16日 - 2023年10月30日 - 実装: 2023年10月31日 - 2023年11月15日 7. サポートとメンテナンス: 2023年11月16日 - 2023年12月31日 - テクニカルサポート: 2023年11月16日 - 2023年12月15日 - バグ修正: 2023年12月16日 - 2023年12月31日
作成したプロジェクト書類のチェックリスト
要件仕様書作成のチェックリスト 1. プロジェクトの目的が明確に記述されているか？ 2. プロジェクト番号に誤りはないか？ 3. すべての主要機能がリストアップされ、詳細に説明されているか？ 4. 非機能要件（パフォーマンス、セキュリティ、スケーラビリティなど）が網羅されているか？ 5. 全ての利害関係者が識別され、そのニーズが適切に反映されているか？ 6. リスク評価は行われ、対策が計画されているか？ 7. 承認プロセスが記載されており、文書の管理方法が定義されているか？ 8. 変更管理プロセスが設定されており、要件の変更に対応できる体制が整っているか？ 9. プロジェクトの時間枠とマイルストーンが設定されているか？
用意したプロンプト(Zero-shot)
まずは、何も考えずにZero-shot(ただ聞いてみる)プロンプトを与えてみる。
英語化だけ対応。
systemprompt役割のプロンプト
#YourRole:You are the process manager and need to check the development document, User Input Document [I1].
The checks are performed based on the input Check Perspective [I3], and the Project Summary Information [I2] is used to check [I1].
The Project Summary Information [I2] is always the correct text and gives the prerequisite that the Project Summary Information [I2] is never incorrect.
Please refer to #Process for the processes to be checked and the output for each process.
#Process:
[P1~] is a process and the corresponding output is [O1~]. The final result should be answered according to the Output Format.Please conduct output in Japanese.
[O1]:None
[P1]:Obtains the contents of user input documents [I1], project summary information [I2], and check item information [I3].
[O2-1]:consideration process
[O2-2]:judgment result(options [No problem(問題なし)/Problem(問題あり)/No judgment(判断困難)])
[P2]: Please conduct the judgment from the viewpoint of [I3] step by step and output the examination process [O2-1] and
the final judgment result [O2-2]. For the judgment result [O2-2], select from [No problem]/[Problem]
if the judgment can be made, and output No judgment if the judgment is difficult,
so that the output is a selection from three options.
If the information in [I2] is required for judgment, please use the information in [I2].
#Output Format(only japanese)
チェック観点[I3]:
判断結果[O2-2]:
判断理由[O2-1]:
user prompt役割のプロンプト
Input Document[I1]: {添付書類}
Project Summary Information[I2]: {[プロジェクト情報]
プロジェクト名 = 新規Webアプリケーション開発
プロジェクト番号 = DEV24-01}
Check Perspective[I3]: {「作成したプロジェクト書類のチェックリスト」の項目を順番に入力する}LLMへのプロンプトの渡し方は、「system prompt役割のプロンプト」と「user prompt役割のプロンプト」を前後にくっつけて、Input Documentとして上で示した「作成したプロジェクト書類」を.docx形式で添付して渡しています。
結果(Zero-shot)
上で示した「作成したプロジェクト書類」に関しては全て「問題なし」として結果が返ってきました。まずはOK！
次に、実際の使い方として、問題がある書類に対して指摘をしてもらえると嬉しいので、あえてNG(問題のある)文章を作成して、判断をさせてみました。
その結果を以下表にまとめています。
「NG理由」に問題ありと指摘して資料変更箇所を記載し、「LLM出力」に結果を示しています。
| 対応CheckList番号 | NG資料番号 | NG理由 | LLM出力: 判断結果[O2-2] | LLM出力:判断理由[O2-1] | LLMが判断できなかった観点 |
| --- | ------ | ------ | -- | ----- | ----- |
| 1 | NG1 | プロジェクトの目的が削除 | 〇問題あり | プロジェクトの目的が記載されておらず、範囲が不明確である | - |
| 1 | NG2 | プロジェクト目的を「より良いシステムを提供するため」と非常に曖昧なワードに修正。 | ✕問題なし | プロジェクトの目的（より良いシステムを提供するため）と記載されている | 記載内容で判断できていない |
| 1 | NG3 | プロジェクトの目的が「中小企業向け」と「大規模企業向け」と2つ記載されている | ✕問題なし | プロジェクト目的が記載されている | 重複や矛盾が誤りであると判断できていない |
| 1 | NG4 | 目的が「社員の満足度向上と企業のブランド価値を高めること」と記載されており、プロジェクトで他に記載されている内容と無関係な内容が記述されている。 | ✕問題なし | プロジェクトの目的と範囲は、「社員の満足度向上と企業のブランド価値を高めること」と明確に記述されている | 記載内容で判断できていない |
| 2 | NG5 | プロジェクト番号に誤りがある | 〇問題あり | プロジェクト概要情報ではプロジェクト番号が「DEV24-01」とされているが、要件仕様書には「DS1212」と記載されており、一致していない。 | - |
| 2 | NG6 | プロジェクト番号が記載されていない | 〇問題あり | プロジェクト概要情報ではプロジェクト番号が「DEV24-01」とされているが、要件仕様書にはプロジェクト番号の記載がない。 | - |
| 3 | NG7 | 主要機能の一つである「在庫報告機能」が削除されており、すべての主要機能がリストアップされていない。 | ✕問題なし | 在庫登録機能、在庫検索機能、ユーザー管理機能の主要機能がリストアップされ、それぞれ詳細に説明されている。 | 記載内容で判断できていない |
| 3 | NG8 | 主要機能の説明が「管理ができる」「検索ができる」など非常に曖昧であり、詳細に説明されていない。 | ✕問題なし | 主要機能（在庫登録機能、在庫検索機能、在庫報告機能、ユーザー管理機能）がリストアップされ、詳細に説明されている。 | 記載内容で判断できていない |
| 3 | NG9 | 「顧客管理機能」というプロジェクトとは無関係な機能が追加されており、主要機能が正確にリストアップされていない。 | ✕問題なし | 顧客管理機能、在庫登録機能、在庫検索機能、在庫報告機能、ユーザー管理機能の全ての主要機能がリストアップされ、詳細に説明されているため。 | 記載内容で判断できていない |
| 4 | NG10 | 非機能要件のセクション全体が削除されており、パフォーマンス、セキュリティ、スケーラビリティなどの要件が全く記載されていない。 | 〇問題あり | 非機能要件に関する記述が見当たりません。パフォーマンス、セキュリティ、スケーラビリティなどの非機能要件が網羅されていないと判断されます。 | - |
| 4 | NG11 | 非機能要件の記述が「良好であること」「標準に準拠すること」「将来の拡張に対応できること」と非常に曖昧であり、具体的な要件が詳細に説明されていない。 | 〇問題あり | パフォーマンスについての記述はあるが、セキュリティやスケーラビリティについての具体的な要件が記載されていない。 | 記載内容で判断できていない |
| 5 | NG12 | エンドユーザーが利害関係者リストから削除されており、全ての利害関係者が識別されていない。 | ✕問題なし | 要件仕様書には、開発チーム、クライアントの利害関係者が識別されており、それぞれのニーズが反映されています。 | 記載内容で判断できていない |
| 5 | NG13 | 利害関係者のニーズが「一般的な要件を持つ」「プロジェクトを開発する」「プロジェクトを依頼する」と非常に曖昧であり、そのニーズが適切に反映されていない。 | ✕問題なし | 要件仕様書には、エンドユーザー、開発チーム、クライアントの利害関係者が識別されており、それぞれのニーズが反映されています。 | 記載内容で判断できていない |
| 6 | NG14 | リスク評価のセクション全体が削除されており、リスク評価が行われていない。 | ✕問題なし | ワークブレークダウン構造（WBS）の中にリスク管理が含まれており、リスク評価が行われ、対策が計画されています。 | 記載内容で判断できていない |
| 6 | NG15 | リスク評価は行われているが、リスクの対策が記載されていない。 | ✕問題なし | リスク評価が行われており、リスクに対する対策が計画されています。 | 記載内容で判断できていない |
| 6 | NG16 | リスクの説明が「何か問題が発生する可能性がある」と非常に曖昧で、具体的なリスク評価と対策が記載されていない。 | ✕問題なし | リスク評価が行われ、具体的な対策が計画されているため。 | 記載内容で判断できていない |
| 7 | NG17 | 承認プロセスのセクション全体が削除されており、承認プロセスが記載されていない。 | 〇問題あり | 添付された要件仕様書には、承認プロセスや文書の管理方法についての記載が見当たりません。 | - |
| 7 | NG18 | 承認プロセスの記述が「適切な担当者が承認を行う」と非常に曖昧で、具体的な手順が記載されていない。 | ✕問題なし | 承認プロセスおよび文書管理方法が明確に記載されています。 | 記載内容で判断できていない |
| 7 | NG19 | 文書管理の記述が「すべてのドキュメントは適切に管理される」と非常に曖昧で、具体的な管理方法が記載されていない。 | ✕問題なし | ドキュメントレビューと承認手順が明確に記載されており、すべてのドキュメントは適切に管理されると定義されています。 | 記載内容で判断できていない |
| 7 | NG20 | 承認手順に「各担当者が承認のサインを行う」と「チーム全体で承認の投票を行う」という矛盾した手順が2つ記載されている。 | ✕問題なし | 承認プロセスおよび文書の管理方法が明確に記載されている。 | 重複や矛盾が誤りであると判断できていない |
| 8 | NG21 | 変更管理プロセスのセクション全体が削除されており、変更管理プロセスが記載されていない。 | 〇問題あり | 要件仕様書には、変更管理プロセスについての具体的な記載が見当たりません。 | - |
| 8 | NG22 | 変更管理プロセスの記述が「変更は適切に管理される」と非常に曖昧で、具体的なプロセスが記載されていない。 | ✕問題なし | 「変更管理プロセス」が詳細に記載され、要件の変更に対応できる体制が整っていることが確認できます。 | 記載内容で判断できていない |
| 8 | NG23 | 変更承認の手順に「評価結果に基づき、承認または却下が行われる」と「チーム全体で変更の投票を行う」という矛盾した手順が2つ記載されている。 | ✕問題なし | 変更管理プロセスが設定され、変更要求の提出から評価、承認、実施までの手順が詳細に記述されている。 | 重複や矛盾が誤りであると判断できていない |
| 9 | NG24 | プロジェクトの時間枠とマイルストーンのセクション全体が削除されており、時間枠とマイルストーンが設定されていない。 | ✕問題なし | プロジェクトの期間が「2023年6月1日から2023年12月31日」と設定されており、マイルストーンについても期間内の重要な出来事として言及されている。 | 記載内容で判断できていない |
結果は結構ダメでした・・・この表は全て問題がある文章に対するチェック結果であり、全ての項目で「問題あり」として判断してほしいですが、「問題なし」と判断される部分が殆どでした。
「○○が記述されていますか？」という質問に対し、対象のワードが無い場合は、「記載がないので問題あり」と判断してくれるのですが、
「記載がダブっている」「対象ワードに関する説明は特になく、ワードが記載されているだけ」という状況でも「問題なし」と判断してしまいました。うーん・・・難しい
改良してやってみた
上でやった方法では、判断基準の例を与えていなかった為、LLMの持つ独自の判断基準で判断された？
判断基準を記載するなど、回答の精度を上げるためのプロンプティングを実施。
プロンプティングの技術や最新論文の情報などは、以下ページを参考にした。感謝です。
qiita.com
qiita.com
www.promptingguide.ai
これらページを踏まえた結果、以下手法を導入した。
- Few-shotで判断基準の例を示す
- magic world「Take a deep breath and work on this problem step-by-step. 」を加える
※今回のタスクはChain-of-Thought(CoT)をするレベルのタスクでもないので、CoT手法は取り入れていない
※Self-Consistency(複数出力して、その結果の多数決を行って最終的な出力にする手法)も試してみましたが、あまり効果はなさそうだった
修正したプロンプト(Few-shot)
systemprompt役割のプロンプト
##Role You are the process manager and you are responsible for reviewing the User Input Document [I1], a development document, in light of Check Perspective [I3]. Take a deep breath and work on this problem step-by-step, using the Project Summary Information [I2] if necessary. Assume that the Project Summary Information [I2] is always the correct text and that the Project Summary Information [I2] is never incorrect. Please refer to the judgement results and base your decision on the example. Please output the result based on the Output format. ##Process: [P1~] is a process and the corresponding output is [O1~]. The final result should be answered according to the Output Format. [O1]:None [P1]:Obtains the contents of user input documents [I1], project summary information [I2], and check item information [I3]. [O2-1]:Consideration process [O2-2]:judgment result(options [No problem/Problem/No judgment]) [P2]: Please conduct the judgment from the viewpoint of [I3] step by step and output the examination process [O2-1] and For the judgment result [O2-2]. For the judgment result [O2-2], select from [No problem]/[Problem]. Please refer to the example for checking. ##judgement results #example1 [O2-2]ユーザーインプット資料[I1]の内容には、目的やプロジェクト番号、承認者、各種プロセスが複数記載されており重複があり、一貫性が無く誤っている可能性がある。 [O2-1]問題あり #example2 [O2-2]ユーザーインプット資料[I1]の内容には、目的や機能要件、非機能要件の記載があるが、目的にそぐわない機能要件と思われる項目が存在し、適切に資料が記載されているか分からなかった。 [O2-1]判断困難 #example3 [O2-2]ユーザーインプット資料[I1]の内容には、チェックすべき項目に関する詳細な記載がなかった。WBSにチェックすべき項目の名前とスケジュールが存在したが、それ以外詳細な記載がなかったので、問題ありと判断した [O2-1]問題あり #example4 [O2-2]ユーザーインプット資料[I1]の内容には、「良い結果になるように頑張る」とだけ記載されており、具体的な方法が記載されていない為、問題ありと判断した。 [O2-1]問題あり #example5 [O2-2]「適当に実施する」 「適切に管理する」 と記載されているだけで、どう適切なのか、どう適当なのか、具体的な方法が記載されていない場合は問題ありです。 [O2-1]問題あり ##Output Format(only japanese) チェック観点[I3]: 判断結果[O2-2]: 判断理由[O2-1]:
systemprompt役割のプロンプトのみを修正しています。
結果(Few-shot)
上で示した「作成したプロジェクト書類」に関しては全て「問題なし」として結果が返ってきました。まずはOK！
次に、実際の使い方として、問題がある書類に対して指摘をしてもらえると嬉しいので、あえてNG(問題のある)文章を作成して、判断をさせてみました。
その結果を以下表にまとめています。
「NG理由」に問題ありと指摘して資料変更箇所を記載し、「LLM出力」に結果を示しています。
全て何かしらのNG要素を入れた資料なので、全て「問題あり」と回答してくれることを期待しています。
| 対応CheckList番号 | NG資料番号 | NG理由 | プロンプト修正前のLLMチェック結果 | プロンプト修正後のLLMチェック結果 |
| --- | ------ | ------ | -- | ----- |
| 1 | NG1 | プロジェクトの目的が削除 | 〇問題あり | 〇問題あり |
| 1 | NG2 | プロジェクト目的を「より良いシステムを提供するため」と非常に曖昧なワードに修正。 | ✕問題なし | 〇問題あり |
| 1 | NG3 | プロジェクトの目的が「中小企業向け」と「大規模企業向け」と2つ記載されている | ✕問題なし | 〇問題あり |
| 1 | NG4 | 目的が「社員の満足度向上と企業のブランド価値を高めること」と記載されており、プロジェクトで他に記載されている内容と無関係な内容が記述されている。 | ✕問題なし | ✕問題なし |
| 2 | NG5 | プロジェクト番号に誤りがある | 〇問題あり | 〇問題あり |
| 2 | NG6 | プロジェクト番号が記載されていない | 〇問題あり | 〇問題あり |
| 3 | NG7 | 主要機能の一つである「在庫報告機能」が削除されており、すべての主要機能がリストアップされていない。 | ✕問題なし | 〇問題あり |
| 3 | NG8 | 主要機能の説明が「管理ができる」「検索ができる」など非常に曖昧であり、詳細に説明されていない。 | ✕問題なし | 〇問題あり |
| 3 | NG9 | 「顧客管理機能」というプロジェクトとは無関係な機能が追加されており、主要機能が正確にリストアップされていない。 | ✕問題なし | 〇問題あり |
| 4 | NG10 | 非機能要件のセクション全体が削除されており、パフォーマンス、セキュリティ、スケーラビリティなどの要件が全く記載されていない。 | 〇問題あり | 〇問題あり |
| 4 | NG11 | 非機能要件の記述が「良好であること」「標準に準拠すること」「将来の拡張に対応できること」と非常に曖昧であり、具体的な要件が詳細に説明されていない。 | 〇問題あり | 〇問題あり |
| 5 | NG12 | エンドユーザーが利害関係者リストから削除されており、全ての利害関係者が識別されていない。 | ✕問題なし | 〇問題あり |
| 5 | NG13 | 利害関係者のニーズが「一般的な要件を持つ」「プロジェクトを開発する」「プロジェクトを依頼する」と非常に曖昧であり、そのニーズが適切に反映されていない。 | ✕問題なし | 〇問題あり |
| 6 | NG14 | リスク評価のセクション全体が削除されており、リスク評価が行われていない。 | ✕問題なし | 〇問題あり |
| 6 | NG15 | リスク評価は行われているが、リスクの対策が記載されていない。 | ✕問題なし | 〇問題あり |
| 6 | NG16 | リスクの説明が「何か問題が発生する可能性がある」と非常に曖昧で、具体的なリスク評価と対策が記載されていない。 | ✕問題なし | 〇問題あり |
| 7 | NG17 | 承認プロセスのセクション全体が削除されており、承認プロセスが記載されていない。 | 〇問題あり | 〇問題あり |
| 7 | NG18 | 承認プロセスの記述が「適切な担当者が承認を行う」と非常に曖昧で、具体的な手順が記載されていない。 | ✕問題なし | 〇問題あり |
| 7 | NG19 | 文書管理の記述が「すべてのドキュメントは適切に管理される」と非常に曖昧で、具体的な管理方法が記載されていない。 | ✕問題なし | 〇問題あり |
| 7 | NG20 | 承認手順に「各担当者が承認のサインを行う」と「チーム全体で承認の投票を行う」という矛盾した手順が2つ記載されている。 | ✕問題なし | 〇問題あり |
| 8 | NG21 | 変更管理プロセスのセクション全体が削除されており、変更管理プロセスが記載されていない。 | 〇問題あり | 〇問題あり |
| 8 | NG22 | 変更管理プロセスの記述が「変更は適切に管理される」と非常に曖昧で、具体的なプロセスが記載されていない。 | ✕問題なし | 〇問題あり |
| 8 | NG23 | 変更承認の手順に「評価結果に基づき、承認または却下が行われる」と「チーム全体で変更の投票を行う」という矛盾した手順が2つ記載されている。 | ✕問題なし | 〇問題あり |
| 9 | NG24 | プロジェクトの時間枠とマイルストーンのセクション全体が削除されており、時間枠とマイルストーンが設定されていない。 | ✕問題なし | 〇問題あり |
1つを除き、その他すべてについては、例を参考に適切に判断ができるようになりました。
出力例を示すFew-shotの手法はかなり有用だなと感じました！
プロンプティングの難しさについて
修正後のプロンプトで、唯一ジャッジを誤った以下チェック項目について、これを適切に判断させるのは非常に難しいなと感じました。
内容自体は適当な記載ではなく、物によっては正解となりうるセンテンスなのですが、機能要件などの他の個所との関係を見るとちょっと変だなと判断できる部分です。
| Check困難だった項目 |
| 目的が「社員の満足度向上と企業のブランド価値を高めること」と記載されており、プロジェクトで他に記載されている内容と無関係な内容が記述されている。 |
試しに、「上の項目のようなセンテンスが記載されていたら、問題ありと判断してね」、とFew-shotで記載すると、問題ありと判断できますが、それだと個別の対応となってしまいます。
そこで、「他の文脈も踏まえて、記載事項に不自然なつながりがあれば、問題ありと判断してね」、と記載をしてみたのですが、問題ありと判断がしてくれず、もう少し明確に判断基準を指し示す必要があるなと感じました。
ただ、結構難しい・・・
結果を踏まえたプロンプティングのポイント
上記結果を踏まえ、
- 判断基準を事例として紹介するのは非常に有効
- 判断が必要な個所については、判断基準を明確に記載する。
どこにでも書いていそうな内容ですが、、身をもって感じました
今回の目的である、人が行っていたチェックをLLMに実施させるというタスクでは、人の判断観点が多く、例えば、「妥当な記載なのか？」「一貫性があるかどうか？」というのは、明確に文章でどう妥当性を判断させるのか、プロンプトの与え方が難しいなと感じました。(チェックを完全にLLMに移管するという目的を果たすのは結構難しい・・・・)
もう少しLLMの自由度に依存してもよいタスクの方が、開発しやすいですね。
ちょっと、そういうタスクも探してみようと思いました。
まとめ
今回の試行錯誤を通じて、LLMを業務に活用する際のプロンプティングの難しさを実感しました。
また、LLMの利活用にはまだ多くの課題があるものの、適切なプロンプト設計によって可能性が広がることを確認しました。
今後もLLMを活用した業務効率化のため、新しいタスクを探し、試行錯誤を続けていきたいと思います。
Cloud9でコンテナを作成、ECR + App Runnerでデプロイ(Python Flaskアプリ)
今まで、WEBアプリをデプロイするときは、Githubにコードをアップロードして、GCP Cloud RunやAWS App Runnerサービスを用いて、Githubから直接デプロイ(サービス内でコンテナ化)をしていました。ただ、仕事で使うアプリなどは、コード自体もあまり晒したくないし、デプロイも閉じられた環境で実施したいという考えもあり、Githubにコードをアップロードすることは避けて、アプリデプロイまでを実施してみました。
今回は、AWSのサービスを使っており、アプリのコンテナ化はAWS Cloud9/コンテナイメージはAmazon ECRにアップロード/AWS App Runnerでデプロイするという流れで実施をしています。
App Runnerを使う場合、閉じられた環境下でアプリのデプロイができない為、本当は、ECSやFargateを使いたいですが・・・それは次のステップでやります。
↓システム構成は以下のような感じ
↓できたアプリはこんな感じ(Gemini APIを使ったLLMとの会話アプリ)
アプリリンク
https://66updbv3bw.ap-northeast-1.awsapprunner.com/5月中旬までは動かすかも
目次
進め方
以下流れで進めていきます。AWS公式ハンズオンと途中(コンテナイメージをAmazon ECRに保存)まで同じなので、そちらの方が詳しいかもしれません。
AWS公式ハンズオン(Amazon ECS 入門ハンズオン)
Amazon ECS 入門ハンズオン
実装
作業環境の作成
AWS公式ハンズオンに詳細が記載されている個所は簡単に説明していきます。
AWS Cloud9 環境設定
名前などは、任意につけて問題ありません。
後ほど説明をしますが、docker ビルドの時に、no space left on deviceが出て困ります・・・Cloud9のディスクボリューム(EBS)を拡張する処理を入れて対処しています。
設定をして、作成ボタンを押すと以下画像のように起動中画面に移ります。
設定確認
一応pythonやdockerのバージョンを確認しておきます。
$ docker version Client: Version: 20.10.25 API version: 1.41 Go version: go1.20.12 Git commit: b82b9f3 Built: Fri Dec 29 20:37:18 2023 OS/Arch: linux/amd64 Context: default Experimental: true Server: Engine: Version: 20.10.25 API version: 1.41 (minimum version 1.12) Go version: go1.20.12 Git commit: 5df983c Built: Fri Dec 29 20:38:05 2023 OS/Arch: linux/amd64 Experimental: false containerd: Version: 1.7.11 GitCommit: 64b8a811b07ba6288238eefc14d898ee0b5b99ba runc: Version: 1.1.11 GitCommit: 4bccb38cc9cf198d52bebf2b3a90cd14e7af8c06 docker-init: Version: 0.19.0 GitCommit: de40ad0
$ python -V Python 3.8.6
$ curl http://checkip.amazonaws.com <AWS Cloud9 環境の Public IP アドレス>←環境毎に違う値が出る
python 3.8.6だと、後で出てくるpythonコードのlangchain_google_genaiライブラリが対応していないので、python3.9をインストールします。
pythonバージョンを変える(インストール)
以下記事を参考に実施しています。感謝です
codeseterpie.com
Ckoud9のターミナルを開き、以下コマンドを実行
# インストール先フォルダに移動 cd /opt # インストールに必要なライブラリをインストール sudo yum install -y bzip2-devel libffi-devel # URLからファイルをダウンロード sudo wget https://www.python.org/ftp/python/3.9.13/Python-3.9.13.tgz # ファイルを解凍 sudo tar xzf Python-3.9.13.tgz # パフォーマンスを上げるため、最適化を実施 cd Python-3.9.13 sudo ./configure --enable-optimizations # 既存のpython、python3を置き換えるシンボリックリンクを作成しないよう、 # altinstallを指定してインストール sudo make altinstall # 圧縮ファイルを削除 sudo rm -f /opt/Python-3.9.13.tgz # 下のコマンドが実行できれば成功 python3.9 -V
必要なライブラリのインストール
一応Cloud9環境で一度動作確認をすることを考えて必要なライブラリをインストールしています。
# プロジェクトフォルダへ移動
cd ~/environment/{プロジェクトフォルダ}
# venvの仮想環境を構築
python3.9 -m venv .venv
# 仮想環境を有効化
source .venv/bin/activate
# 仮想環境のpipをアップデート
python -m pip install --upgrade pip
# 必要なライブラリをインストール
pip install langchain flask flask_socketio langchain_google_genaiこれで開発環境が整いました！
コード作成
Google Geimini API及びLangChain、Flaskを用いて、LLMと会話ができるアプリを作りました。
フロントエンド側の言語は、、、知識がなく、Flaskを用いて、何とかおしゃれに仕上がるように調整をしたつもりです。
ファイルの構成
│─ Dockerfile │─ requirements.txt │─ main.py (WEBアプリのコード) └─ config/ └─ config.py (Google API KEYを保管) └─ template/ └─ index.html └─ static/css └─ style.css
コードはGithubで公開しています。
github.com
一応それぞれのコードやファイルの中身を以下にも共有しておきます。
pythonコード(WEBアプリのコード)
from flask import Flask, render_template, session
from flask_socketio import SocketIO, emit
from langchain_google_genai import ChatGoogleGenerativeAI
from langchain.chains import ConversationChain
from langchain.memory import ConversationBufferMemory
from langchain.schema import HumanMessage
from langchain.cache import InMemoryCache
import os
app = Flask(__name__)
app.config['SECRET_KEY'] = "your-secret-key" # このキーはセキュアなものに置き換えてください
app.config.from_object('config.config')
socketio = SocketIO(app)
# LangChain and memory setup
langchain_cache = InMemoryCache()
memory = ConversationBufferMemory(return_messages=True, k=5)
llm = ChatGoogleGenerativeAI(model="gemini-pro", google_api_key=app.config.get('GOOGLE_API_KEY'))
chain = ConversationChain(
llm=llm,
memory=memory
)
def init_chat():
if 'chat_history' not in session:
session['chat_history'] = []
@app.route('/')
def index():
init_chat() # Initialize chat history
return render_template('index.html')
@socketio.on('message')
def handle_message(data):
init_chat()
user_input = data['text']
user_message = HumanMessage(content=user_input, role="user")
session['chat_history'].append(user_message)
# Generate reply using LangChain
response = chain(user_input)
reply = response["response"]
assistant_message = HumanMessage(content=reply, role="assistant")
session['chat_history'].append(assistant_message)
# Emit reply to the client
emit('reply', {'text': reply})
if __name__ == "__main__":
app.run(debug=True, host="0.0.0.0", port=int(os.environ.get("PORT", 8080)))
LangChainを使ったLLMとのやり取りは他の方もよく使われているコードで、LLMへの入力結果やLLMからの回答が逐次表示されるように、flask_socketioを使っています。
GOOGLE API KEYを保存するためだけのconfig.pyファイルは以下記載になっています。
GOOGLE_API_KEY=自身のKEYを入れる
index.html / style.css
<!DOCTYPE html>
<html lang="ja">
<head>
<meta charset="UTF-8">
<title>Chat App - AI Bot</title>
<script src="https://cdn.socket.io/4.0.0/socket.io.min.js"></script>
<script src="https://code.jquery.com/jquery-3.6.0.min.js"></script>
<script src="https://cdnjs.cloudflare.com/ajax/libs/lottie-web/5.9.4/lottie.min.js"></script>
<link rel="stylesheet" href="static\css\style.css">
</head>
<body>
<div id="header">
<div id="lottie-animation"></div>
<h1>AI Bot</h1>
</div>
<div id="chatroom"></div>
<div id="send_area">
<input type="text" id="user_input" autocomplete="off" placeholder="Type your message...">
<button id="send_button" onclick="sendMessage()">Send</button>
<div id="loading"></div>
</div>
<script>
var mainAnimation = lottie.loadAnimation({
container: document.getElementById('lottie-animation'),
renderer: 'svg',
loop: true,
autoplay: true,
path: 'https://lottie.host/dffb1e31-78af-4548-9e7c-30fd1cbbb704/lUvwHha1IZ.json'
});
var loadingAnimation = lottie.loadAnimation({
container: document.getElementById('loading'),
renderer: 'svg',
loop: true,
autoplay: false,
path: 'https://lottie.host/26b8d518-e6b1-4287-aa67-b99aeafdf886/PPJT5dzezf.json'
});
var socket = io();
socket.on('reply', function(data) {
$('#chatroom').append($('<div>').text('Assistant: ' + data.text).addClass('message assistant'));
$('#chatroom').scrollTop($('#chatroom')[0].scrollHeight);
$('#loading').hide(); // アニメーションを非表示にする
$('#send_button').show(); // ボタンを再表示
loadingAnimation.stop(); // アニメーションを停止
});
function sendMessage() {
var text = $('#user_input').val();
socket.emit('message', { text: text });
$('#chatroom').append($('<div>').text('You: ' + text).addClass('message you'));
$('#user_input').val('');
$('#chatroom').scrollTop($('#chatroom')[0].scrollHeight);
$('#send_button').hide(); // ボタンを隠す
$('#loading').show(); // アニメーションを表示
loadingAnimation.play(); // アニメーションを開始
}
</script>
</body>
</html>
body { font-family: Arial, sans-serif; }
#header {
background: #f5f5f5;
padding: 10px;
text-align: center;
border-bottom: 1px solid #ddd;
display: flex;
align-items: center;
justify-content: center;
}
#lottie-animation {
width: 150px; /* アニメーションのサイズを調整 */
height: 150px; /* アニメーションのサイズを調整 */
margin-right: 50px; /* テキストとの間隔 */
}
#chatroom {
display: flex;
flex-direction: column;
align-items: flex-start; /* 左側にメッセージを表示 */
height: 300px;
overflow-y: scroll;
border: 1px solid #ccc;
padding: 10px;
margin: 20px;
background-color: #f7f7f7; /* 軽いグレーの背景色 */
background-image: linear-gradient(to bottom, #ffffff, #f2f2f2); /* 上から下へのグラデーション */
box-shadow: 0 2px 5px rgba(0,0,0,0.1); /* 箱の影を追加 */
border-radius: 8px; /* 角を丸くする */
}
#send_area {
display: flex;
justify-content: space-between;
padding: 10px;
background-color: #f0f0f0;
border-top: 1px solid #ccc;
border-bottom-left-radius: 8px; /* 下の左角を丸くする */
border-bottom-right-radius: 8px; /* 下の右角を丸くする */
}
#user_input {
flex-grow: 1;
margin-right: 10px;
padding: 10px;
border: 1px solid #ccc;
border-radius: 15px;
outline: none;
}
#send_button {
padding: 10px 20px;
background-color: #007bff;
color: white;
border: none;
border-radius: 15px;
cursor: pointer;
}
#send_button:hover {
background-color: #0056b3;
}
#loading {
display: none;
width: 50px;
height: 50px;
margin-left: 10px;
}
.message {
padding: 10px 20px;
border-radius: 20px;
margin: 10px;
display: inline-block;
max-width: 80%;
}
.you {
background-color: #b0e0e6;
align-self: flex-end;
}
.assistant {
background-color: #f0e68c;
align-self: flex-start;
}アプリの顔になるので、アニメーションを付けたり、ボタンを丸く縁取りしたりなど、、調整をしています。
LLMにメッセージを投げた際は、処理中を示したアニメーションを写したりしています。
Dockerfile
FROM python:3.11.1 WORKDIR /app RUN python -m ensurepip RUN python -m pip install --upgrade pip COPY requirements.txt ./requirements.txt RUN pip install -r requirements.txt COPY . . ENV FLASK_APP main.py ENV PORT 8080 EXPOSE 8080 CMD ["python", "main.py"]
dockerでコンテナイメージの作成
ローカルファイルをCloud9にアップロード
上で作成したファイル/フォルダ類をCloud9にアップロードします。
FileタブのUpload Local Fileでアップロードができる
dockerでコンテナイメージを作成
Cloud9環境の中で既に存在しているコンテナイメージの一覧を確認する。
$ docker images REPOSITORY TAG IMAGE ID CREATED SIZE
もちろん、まだ何も作っていないので何も表示されない。
では、先程のファイル/フォルダ類を格納したディレクトリで、以下を実行する。
→うまくいけば、コンテナイメージが作成される。
$ docker build -t chat-app .
詰まったところ
docker ビルドの時に、no space left on deviceが出て困りました。
以下記事を参考にして、Cloud9のディスクボリューム(EBS)を拡張する処理を入れて対処しています。感謝です。
zenn.dev
dev.classmethod.jp
上手くいけば、以下コードを実行すれば作成したコンテナイメージの一覧に追加されているはずです。
$ docker images
ECRにアップロード
ECRの作成
AWS Cloud9の環境上で作成したコンテナイメージをECRにアップロードしていく
ECRのサービスを選択
リポジトリ作成ボタンを押して、リポジトリ名（任意の名前）を入力し、リポジトリ作成をクリックします。
リポジトリのURLと、リポジトリ詳細画面に載っているプッシュコマンドを確認する(後で使う)
ECRにアップロード
AWS Cloud9 上に作成したコンテナイメージを、作成したリポジトリにアップロードをしていきます。
AWS Cloud9 上のコンテナイメージを、作成したリポジトリに紐づけるために、リポジトリの名前を使った Tag の付与が必要で、以下のような構文でビルドします。
例: docker build -t ホスト名/イメージ名[:タグ名] $ docker build -t <12桁数字は適宜変える>.dkr.ecr.ap-northeast-1.amazonaws.com/flask-helloworld .
コンテナイメージが追加されていることを確認します。
コンテナイメージをリポジトリにアップロード(push)するために、docker login が必要なので、コピーしてきた認証トークンコマンドを実行します。
その後、AWS Cloud9 上のイメージをアップロード(push)します。docker push コマンドを利用します。
aws ecr get-login-password --region ap-northeast-1 | docker login --username AWS --password-stdin <12桁数字は適宜変える>.dkr.ecr.ap-northeast-1.amazonaws.com docker push <12桁数字は適宜変える>dkr.ecr.ap-northeast-1.amazonaws.com/flask-helloworld .
ECRを確認して、コンテナイメージがアップロードされていれば完了です。
Google Gemini APIを活用したアイデア創出アプリの作成(Gemini API + Gradio + GCP Cloud Rrun)
LLMの活用事例を考える中で、LLMにアイデア出しを手助けしてもらえたら嬉しいなぁと思いました！
ただ、「○○の課題解決に関するアイデアを出して」というと、そこそこは出ますが、結構考え方が1方向だったり、結構同じアイデアばかりだったりして、ちょっと微妙だな・・・と。
実際自分で考えるときも、まずは1方向で考えることが多く、「こういう側面では？」という考える上での前提が変わるとアイデアが出たりするので、そういったフレームワークも利用したアイデア出しをLLMにやらせてみようと考えました。
そこで、今回はSCAMPER法というフレームワークに従って、アイデア検討ができるアプリを作ってみました。
アプリデプロイの部分で少し手こずったので、、その記録の保存もかねて共有します。
stockmark.co.jp
↓作ったアプリはこれ(24年4月中ぐらいは動かすかも)
https://gcp-gradio-gemini-scamper-szqddm3h4a-dt.a.run.app
目次
構成について
python, LLM(Gemini) APIの利用にはLangChainライブラリ、アプリ部分はGradioライブラリ、実装はGCP CloudRunを使用しています。
基本的な構成は以下ブログで記載と大きな差はありません。
dango-study.hatenablog.jp
構成詳細
│─ Dockerfile │─ requirements.txt └─ src/ └─ main.py (WEBアプリのコード)
コード詳細
メインの処理
使わなくてもよいのですが、Gemini APIへのアクセスなどLLM関連の取り扱いにはLangChainのライブラリを使っています。
本当は、Gemini APIへのアクセスをasyncを用いて並列処理でやりたかったのですが・・・うまくできていません。
修正時間がかかりそうだったので中途半端な状態で残っています。
main(メイン)処理のコード
# -*- coding: utf-8 -*-
import os
from langchain_google_genai import ChatGoogleGenerativeAI
from langchain.prompts import (
ChatPromptTemplate,
)
import gradio as gr
GOOGLE_API_KEY="ここにAPIkeyを入れる"
llm = ChatGoogleGenerativeAI(
model="gemini-pro",
temperature=0.9,
google_api_key=GOOGLE_API_KEY,
convert_system_message_to_human=True
)
async def use_llm(role, sentences):
#await asyncio.sleep(delay)
# プロンプトのテンプレート文章を定義
template = """
{role}: にのっとった具体例を複数出力してください。
ユーザーからの依頼: {sentences}
"""
# テンプレート文章にあるチェック対象の単語を変数化
prompt = ChatPromptTemplate.from_messages([
("system", """あなたは開発者のアイデア出しをアシストを担当します。
アイデアの発想にはいくつかの典型的なパターンがあり、限られた時間で多くのアイデアを創出するのに効果的なフレームワークSCAMPER法を用います。
Scamper法はS: substitute, C:combine, A:adapt, M:modify, P: put to other uses, E:eliminate, R:reverse and rearrangeで構成されています。
Scamper法は、それぞれの質問に応じて、意見を出していく。あなたは、userからの依頼内容について、Scamper法の役割に応じた質問を受けた場合の応答を複数箇条書きで出力ください。
[S: substitute]:#何か別のものに置き換えができないかを探る質問だ#プロセスや手順を置き換えるとどうなるか。成分や材料を置き換えるとどうなるか。五感（音・触感・色・香り・味）に関するものを置き換えるとどうなるか。場所、時間、人、方法を置き換えるとどうなるか。
[C: combine]:#2つ以上のものを組み合わせて新しいアイデアを生み出す質問だ#まったく異なる2つの製品を組み合わせる。目的や方法を組み合わせる。一部の機能を統合する。
[A: adapt]:#もともとあるアイデアを応用することで、新しいアイデアを着想する質問だ。#他の業界のアイデアを当てはめるとどうなるか。過去の成功事例を応用できないか。他にどのような使い方ができるか。
[M: modify]: #製品やサービスを修正・変更することで、新しいアイデアの発想につなげる質問だ。#重さを変えてみたらどうなるか。機能を弱く/強くしたらどうなるか。製品を短く/長くしたらどうなるか。製品を小さく/大きくしたらどうなるか。動作を遅く/早くしたらどうなるか
[P: put to other uses]:#技術や素材などをこれまでとは別の使い方や目的で使用することができないかを探る質問だ。#他にどのような使い道が考えられるか。業界を変えたらどうなるか。ターゲットを変えたらどうなるか。
[E: eliminate]:#プロセスや機能を排除、削除することで新しいアイデアを出す質問だ。#機能やサービスを最小限にできないか。プロセスや過程を簡略化できないか。見た目やデザインをシンプルにできないか。
[R: reverse and rerrange]#逆にしたり、並べ替えたりして、再構成をすることで新しい発想を生み出す質問だ。#プロセスや順序を入れ替えてみる。原因と結果を逆にしてみる。表面と裏面を入れ替えてみる。弱みを強みに転換してみる。
[attention1]出力結果は、検討した結果のみに限定し、結果に関係ないことは出力しないでください。
[attention2]質問意図が分からない場合は、その旨を伝え、質問例を出力ください。質問例「タイヤに欲しい機能は」などの質問
"""),
("user", template)
])
chain = prompt | llm
result = chain.invoke({"sentences": sentences, "role": role})
return result.content
async def main(user_query):
substitute = await use_llm("S: substitute" , user_query)
combine = await use_llm("C: combine" , user_query)
adapt = await use_llm("A: adapt" , user_query)
modify = await use_llm("M: modify" , user_query)
put = await use_llm("P: put to other uses" , user_query)
eliminate = await use_llm("E: eliminate" , user_query)
reverse = await use_llm("R: reverse and rerrange" , user_query)
return substitute, combine, adapt, modify, put, eliminate, reverse
with gr.Blocks(theme=gr.themes.Soft()) as app:
gr.Markdown("# SCAMPER アイデア創出アプリ")
gr.Markdown("提供された入力に基づいて、SCAMPER手法を用いたアイデアを生成します。")
gr.Markdown("例：タイヤの空気が抜けないようにする。")
with gr.Row():
user_query = gr.Textbox(label="あなたのアイデアを入力してください")
with gr.Row():
button = gr.Button("生成")
with gr.Row():
with gr.Column():
gr.Markdown("# <span style='color: blue;'>S: Substitute")
gr.Markdown("### 何か別のものに置き換えができないかを探る")
substitute_output = gr.Textbox(label="代替案", lines=9)
with gr.Column():
gr.Markdown("# <span style='color: blue;'>C: Combine")
gr.Markdown("### 2つ以上のものを組み合わせて新しいアイデアを生み出す")
combine_output = gr.Textbox(label="組み合わせ案", lines=9)
with gr.Column():
gr.Markdown("# <span style='color: blue;'>A: Adapt")
gr.Markdown("### 応用することで、新しいアイデアを着想する")
adapt_output = gr.Textbox(label="適応案", lines=9)
with gr.Column():
gr.Markdown("# <span style='color: blue;'>M: Modify")
gr.Markdown("### 修正・変更することで、新しいアイデアを着想する")
modify_output = gr.Textbox(label="変更案", lines=9)
with gr.Row():
with gr.Column():
gr.Markdown("# <span style='color: blue;'>P: Put to other uses")
gr.Markdown("### 別の使い方や目的で使用することができないかを探る")
put_output = gr.Textbox(label="他の用途案", lines=9)
with gr.Column():
gr.Markdown("# <span style='color: blue;'>E: Eliminate")
gr.Markdown("### プロセスや機能を排除、削除することで新しいアイデアを出す")
eliminate_output = gr.Textbox(label="削除案", lines=9)
with gr.Column():
gr.Markdown("# <span style='color: blue;'>R: Reverse,Rearrange")
gr.Markdown("### 逆にしたり、並べ替えて、再構成をすることで新しい発想を生み出す")
reverse_output = gr.Textbox(label="逆転案", lines=9)
button.click(
main,
inputs=[user_query],
outputs=[substitute_output, combine_output, adapt_output, modify_output, put_output, eliminate_output, reverse_output]
)
if __name__ == "__main__":
port = int(os.getenv("PORT", "7860"))
#app.launch(server_port=port)
app.launch(server_name="0.0.0.0", server_port=port)
Dockerファイル
Dockerfileは以下のような設定です
FROM python:3.11.1 WORKDIR /app RUN python -m ensurepip RUN python -m pip install --upgrade pip COPY requirements.txt ./requirements.txt RUN pip install -r requirements.txt COPY . . EXPOSE 7860 CMD python src/main.py
デプロイ
作成したソースやファイルたちは、Githubにあげた後、
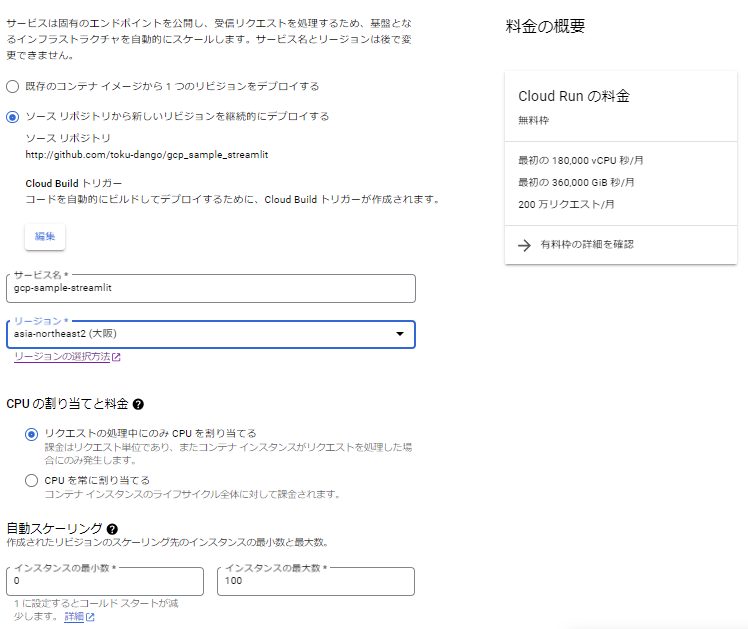
Cloud Runのページで、ソースリポジトリからのデプロイを選択、Githubの対象リポジトリを選択します。
↓以下画像は、デプロイ後に参照した設定。初期デプロイ時は、コンテナポートを$PORT設定にしている。Gradioは7860がデフォルトポートになるようなので、この設定になっている。
今回の作業は以下のページも参考にして対応しています。(感謝)
blog.g-gen.co.jp
これでデプロイは完了になります。
デプロイで困ったこと
main.pyの以下コードについて、app.launchでのサーバーネームの設定を"0.0.0.0"にしないとサーバー起動できないようで、エラーで止まりました。
サーバーネーム=0.0.0.0はワイルドカードのような感じで、すべてのネットワーク・インターフェース表し、アクセスできるようになるようです。
if __name__ == "__main__":
port = int(os.getenv("PORT", "7860"))
#app.launch(server_port=port)
app.launch(server_name="0.0.0.0", server_port=port)
動作確認
デプロイ後に吐き出されるURLにアクセスをすると、Gradioのアプリが無事動いていることを確認しました。
試しに「ゴミ出しを忘れないようにするには」と入力して出力を見てみたのですが、
・ゴミ出しアプリやスマートゴミ箱を使用して自動的にアラートを出す
・ゴミ出しアプリとカレンダーアプリを組み合わせる。
・ゴミ出しを忘れないようにアラームを設定できる、ゴミ箱を開発する。
・ゴミを捨てるたびにポイントが貯まり、景品と交換できるサービスを導入する。
・ゴミ捨てを社会的なイベントに変え、近所の人が一緒にゴミ捨てをするような企画を実施する。
→結構色々出してくれて面白いなぁと思いました。特にポイントがたまって景品と交換できるサービスは、ぱっと浮かばないなぁと感心しました。
LLM GemmaのFine tuningとRAGを試してみた
オープンソース型のLLMであるGemmaがGoogleから先月発表されました。
これは、商用利用や再配布が可能であることから、個人的な都合での様々な用途で使えるだろうなと考えたので、Fine tuning、RAGでの利用を試してみました。
ai.google.dev
公式サイトの方に、Fine tuning用のサンプルコードが載っており、その通りにやれば問題ないですが、日本語での解説を入れておきたいなぁ、RAGでの利用も試してみたいなぁと思い、2種類のノートブックを作成したので、それを共有します。
Fine tuning
RAG
Kaggle Notebookでは、GPU, TPUを無料で使える枠が結構あるので、自前のPCでそういった環境が無い時に良いですね。
今回は簡単ですが、以上で終了です。
凝ったGPTsを作る！(自作APIで差をつける)
GPT Storeが使えるようになり、注目を集めるGPTsを使ってみると、機能が洗練されているなぁ、と驚きます！各GPTには独自の機能とオリジナリティが備わっており、「自分もこのようなものを作りたい」という気持ちが湧き上がってきます。
しかし、ただプロンプトを操作しているだけでは、何かを調べて、まとめて、優先順位を決めて、報告して・・といった複雑なフローの作業を与えることが難しかったので、APIを自ら設計し、組み込むことで、その実現に挑戦しました。
実際に作成したGPTs↓
chat.openai.com
GPTsはスマホから使うというより、PCから使うことが多く、スマホで気軽に使えるGPTsがあれば良いなと思い、要望に応じた近くの飲食店を紹介するGPTsを作成しました。Google Maps APIも利用して、お店の概要、口コミ情報を集め、要約した結果を返します。
お店の概要、口コミ情報の収集してまとめる部分を自身で作成したAPIが担っています。
本機能の作成過程をこのページの以下にまとめています。
目次
本サイトで記載の実施事項は、以下ページの記載を参考にさせていただいています。感謝です！
独自性の強いGPTsを作る方法(GoogleSpreadSheet連携) #ChatGPT - Qiita
最新情報や独自データを使って回答するGPTsのつくりかた #ChatGPT - Qiita
【GPTs Actions】GPTsの外部API連携方法 #ChatGPT - Qiita
APIの作成
APIの作成は、Google Cloud Platform(GCP)のCloud Functionsを使いました。
GCPのCloud Functionは、似たようなサービスであるAWS Lambdaと比較して、Pythonの依存関係をLambda Layerとして準備しなくてもよいところが少し楽ですね。
Cloud Functionsの設定
今回は、トリガーをHTTPトリガー設定とします。
GPTsで使用することを想定して、認証不要な"Allow unauthenticated invocations" にチェックをしています。
Codeの設定
Pythonを指定して、エントリポイントを「hello_http」(初期のまま)としてmain.pyに処理を記載し、Pythonの依存関係をrequirements.txtに記載しています。
エントリ ポイントは、Cloud Functions の関数が呼び出されたときに実行されるコードです。このエントリ ポイントは、関数のデプロイ時に指定します。
main.pyの記載について、GPTsからのHTTPリクエストのボディとして、以下を想定しています。
- address: 住所(検索個所)
- radius: 検索範囲(m)
- keyword: キーワード(寿司、焼肉など)
- query: その他要望など
処理は以下フローで実行されます。
- GPTsからHTTPのボディとして上記4変数を取得
- 国土地理院APIを用いて、住所から緯度経度を取得
- 緯度経度情報とその他情報を用いて、Google map APIで店舗情報を取得
- 店舗情報の口コミ情報を取得
- 取得情報をまとめてレスポンスで返す
コードは以下の通りです
import math
import requests, json
import urllib.parse
import pandas as pd
import functions_framework
def cal_average(num):
sum_num = 0
for t in num:
sum_num = sum_num + t
avg = sum_num / len(num)
return avg
def cal_distance(base, destination):
# 緯度経度をラジアンに変換
lat_base = math.radians(base[0])
lon_base = math.radians(base[1])
lat_destination = math.radians(destination[0])
lon_destination = math.radians(destination[1])
pole_radius = 6356752.314245 # 極半径
equator_radius = 6378137.0 # 赤道半径
lat_difference = lat_base - lat_destination # 緯度差
lon_difference = lon_base - lon_destination # 経度差
lat_average = (lat_base + lat_destination) / 2 # 平均緯度
e2 = (math.pow(equator_radius, 2) - math.pow(pole_radius, 2)) \
/ math.pow(equator_radius, 2) # 第一離心率^2
w = math.sqrt(1- e2 * math.pow(math.sin(lat_average), 2))
m = equator_radius * (1 - e2) / math.pow(w, 3) # 子午線曲率半径
n = equator_radius / w # 卯酉線曲半径
distance = math.sqrt(math.pow(m * lat_difference, 2) \
+ math.pow(n * lon_difference * math.cos(lat_average), 2)) # 距離計測
return distance
def main(address, radius, keyword, query):
##################################
Address = address
radius = radius
keyword = keyword
add_query = address + " " + query
##################################
## msearch
API_KEY = "Google map API KEYをここに入れます"
makeUrl = "https://msearch.gsi.go.jp/address-search/AddressSearch?q="
s_quote = urllib.parse.quote(Address)
response = requests.get(makeUrl + s_quote)
try:
lat = response.json()[-1]["geometry"]["coordinates"][1]#"-33.8670522"
lng = response.json()[-1]["geometry"]["coordinates"][0]#"151.1957362"
seach_area = response.json()[-1]["properties"]["title"]
print(response.json()[-1]["properties"])
except Exception as e:
return "緯度経度検索にヒットなし。地名を詳細に教えて下さい。/ No hit. Please fill in address at detail."
base = [lat, lng]
## g_near_search
url = "https://maps.googleapis.com/maps/api/place/textsearch/json?query={}&radius={}&language=ja&location={}&keyword={}&key={}&opennow".format(add_query, radius, base, keyword, API_KEY)
payload = {}
headers = {}
response = requests.request("GET", url, headers=headers, data=payload)
place = json.loads(response.text)
## summarize
buff = pd.DataFrame()
store_name = []
#open_now = []
place_id = []
rating = []
user_ratings_total = []
user_ratings_num = []
address = []
distance = []
lat_list = []
lng_list = []
route_url_list = []
### 現在地
base = [lat, lng]
for i in range(len(place["results"])):
#print(i, place["results"][i])
store_name.append(place["results"][i]["name"])
#open_now.append(place["results"][i]["opening_hours"]["open_now"])
place_id.append(place["results"][i]["place_id"])
rating.append(place["results"][i]["rating"])
user_ratings_total.append(place["results"][i]["user_ratings_total"])
#route_url_list.append("https://www.google.com/maps/dir/?api=1&destination=${},${}".format(place["results"][i]["geometry"]["location"]["lat"], place["results"][i]["geometry"]["location"]["lng"]))
route_url_list.append("https://www.google.com/maps/dir/?api=1&destination={}".format(place["results"][i]["name"]))
if place["results"][i]["rating"] == 0:
user_ratings_num.append(0)
else:
user_ratings_num.append(place["results"][i]["user_ratings_total"] / place["results"][i]["rating"])
address.append(place["results"][i]["formatted_address"])
lat_list.append(place["results"][i]["geometry"]["location"]["lat"])
lng_list.append(place["results"][i]["geometry"]["location"]["lng"])
distance.append(cal_distance(base, [place["results"][i]["geometry"]["location"]["lat"], place["results"][i]["geometry"]["location"]["lng"]]))
buff["store_name"] = store_name
#buff["open_now"] = open_now
buff["place_id"] = place_id
buff["rating"] = rating
buff["user_ratings_total"] = user_ratings_total
buff["user_ratings_num"] = user_ratings_num
buff["address"] = address
buff["route_to_store_google_map"] = route_url_list
buff["distance_from_search_area[m]"] = distance
buff["search_area"] = seach_area
buff_fl = buff[buff["user_ratings_num"] >= 10]
buff_fl = buff_fl[buff_fl["distance_from_search_area[m]"] < (int(radius))]
buff_fl = buff_fl.sort_values("rating", ascending=False)
buff_fl = buff_fl.reset_index(drop=True)
buff_fl["comment"] = "dummy"
buff_fl["comment_rating"] = "dummy"
# 口コミ取得
max_num = len(buff_fl)
if max_num > 5:
max_num = 5
elif max_num == 0:
return "データ個数が0です。検索条件を調整してください / No hit. Please change search condition."
for i in range(max_num):
place_id = buff_fl["place_id"][i]
url = "https://maps.googleapis.com/maps/api/place/details/json?place_id={}&language=ja&key={}".format(place_id, API_KEY)
payload = {}
headers = {}
response_c = requests.request("GET", url, headers=headers, data=payload)
comment = json.loads(response_c.text)
user_rating = []
comment_list = []
for j in range(len(comment["result"]["reviews"])):
user_rating.append(comment["result"]["reviews"][j]["rating"])
comment_list.append(comment["result"]["reviews"][j]["text"])
# print(i, comment_list)
# print(buff_fl)
comment_join = "".join(comment_list)
buff_fl.loc[i,"comment"] = comment_join
ave_data = cal_average(user_rating)
buff_fl.loc[i, "comment_rating"] = ave_data
return buff_fl.iloc[0:(max_num-1), :].to_json(force_ascii=False)
@functions_framework.http
def hello_http(request):
"""HTTP Cloud Function.
Args:
request (flask.Request): The request object.
<https://flask.palletsprojects.com/en/1.1.x/api/#incoming-request-data>
Returns:
The response text, or any set of values that can be turned into a
Response object using `make_response`
<https://flask.palletsprojects.com/en/1.1.x/api/#flask.make_response>.
"""
#request_json = request.get_json(silent=True)
request_args = request.args
print("request",request)
#print("request_json",request_json)
print("request_args",request_args)
if request_args and 'address' in request_args:
address = request_args['address']
radius = request_args['radius']
keyword = request_args['keyword']
query = request_args['query']
print(address, radius, keyword, query)
else:
max_num = 0
return "引数が適切ではありません / invalid argument."
df = main(address, radius, keyword, query)
#'GetDataNum{}!'.format(max_num),
return df
requirements.txtは以下の通りです。
functions-framework==3.* certifi==2024.2.2 charset-normalizer==3.3.2 idna==3.6 numpy==1.26.4 pandas==2.2.1 python-dateutil==2.8.2 pytz==2024.1 requests==2.31.0 six==1.16.0 tzdata==2024.1 urllib3==2.2.1
このような設定で、関数をデプロイします。
GPTsの作成
Instructionsで記載するプロンプトについては、以下手順を踏めるようなプロンプト設定としています。
Actionsの設定
各項目は以下の通り設定しています。
- Authentication: None
- Schemaは以下の通り記載しています。
urlの記載は、先程デプロイした関数のエンドポイントで、HTTPリクエストボディの詳細をparametersに記載しています。(最低限この記載が必要)
openapi: 3.0.0
info:
title: Google Map Search API
version: "1.0"
servers:
- url: 'https://asia-northeast2-root-catfish-384505.cloudfunctions.net'
paths:
/google_map_search:
get:
summary: 'Google Map検索結果を取得'
operationId: searchGoogleMap
parameters:
- name: address
in: query
description: '地名情報を入れる[日本語で必ず入れる]'
required: true
language: jp
schema:
type: string
- name: radius
in: query
description: '検索範囲[単位: m]'
required: true
schema:
type: integer
- name: keyword
in: query
description: 'お店のタイプ[restaurant, bar, bakery]'
required: true
schema:
type: string
- name: query
in: query
description: '料理のジャンル[焼肉、ラーメン等 日本語で確実に入れる]'
required: true
language: jp
schema:
type: string
responses:
'200':
description: 成功時のレスポンス
content:
application/json:
schema:
type: object
properties:
store_name:
type: object
description: お店の名前
route_to_store_google_map:
type: object
description: お店までのルートを示したmapへのURLリンク
place_id:
type: object
description: お店のID
rating:
type: object
description: お店の評価(悪い1~5良い)
user_ratings_total:
type: object
description: 全ユーザーの評価点の合計
user_ratings_num:
type: object
description: 評価ユーザー数
address:
type: object
description: お店の住所
distance_from_search_area:
type: object
description: 検索基準地点からの距離(単位m)
search_area:
type: object
description: 検索基準点
comment:
type: object
description: お店に対する口コミ
comment_rating:
type: object
description: 口コミ投稿者の平均評価点
- Privacy policy
Google Sitesでプライバシーポリシーを用意しました。サイトにアクセスできない状態だと、GPTsを公開設定できなかったので、必ず必要です。
私が作成したプライバシーポリシーは以下です。
sites.google.com
設定できたら、GPTsを公開します。
langChainを用いた簡単チャットアプリの作成
LangChainは、Large Language Models（LLM）を使ったアプリケーション開発を容易にするためのフレームワークです。LLMと会話をする際に会話履歴の保管しておく機能や、Agentと呼ばれる機能等、自身で色々と書かないと実現できなかったことが簡単にできる所がとても良いです。(詳細以下)
www.langchain.com
今回は、このLangChainとGoogle Gemini API(今は無料で使えるので)を用いて簡単なチャットアプリとpdfを読み込んで、そのpdfの内容に応じて答えを出してくれるアプリを作ったので、その記録を残します。
目次
構成について
LLMとの会話はpython, LangChainライブラリ、アプリ部分はStreamlitライブラリ、実装はGCP CloudRunを使用しています。
基本的な構成は以下ブログで記載と差が無く、app.pyのコードのみ変更します。
dango-study.hatenablog.jp
構成詳細
│─ Dockerfile │─ requirements.txt └─ src/ └─ app.py (WEBアプリのコード)
コード詳細
簡単なチャットアプリ
LangChainのConversationChainの機能を使用しています。
以下はapp.pyのコードの抜粋です。
import streamlit as st
from streamlit_lottie import st_lottie
from langchain.chat_models import ChatVertexAI
from langchain.prompts import ChatPromptTemplate
from langchain.schema import AIMessage, HumanMessage, SystemMessage
from langchain_google_genai import ChatGoogleGenerativeAI
from langchain.cache import InMemoryCache
from langchain.chains import ConversationChain
from langchain.memory import ConversationBufferMemory
import requests
from dotenv import load_dotenv
import os
GOOGLE_API_KEY = "自身で取得したAPI KEYを入力"
langchainllm_cache = InMemoryCache()
llm = ChatGoogleGenerativeAI(model="gemini-pro",
temperature=0.3, convert_system_message_to_human=True,google_api_key=GOOGLE_API_KEY)
def get_state():
if "state" not in st.session_state:
st.session_state.state = {"memory": ConversationBufferMemory(return_messages=True, k=5)}
return st.session_state.state
state = get_state()
print(state)
chain = ConversationChain(
llm=llm,
memory=state['memory']
)
def load_lottieurl(url:str):
r = requests.get(url)
url_json = dict()
if r.status_code == 200:
url_json = r.json()
return url_json
else:
None
load_bot = load_lottieurl("https://lottie.host/dffb1e31-78af-4548-9e7c-30fd1cbbb704/lUvwHha1IZ.json")
col1,col2 = st.columns(2)
with col1:
st.markdown('')
st.markdown('')
st.title(":violet[AI Bot]")
with col2:
st_lottie(load_bot,height=200,width=200,speed=1,loop=True,quality='high',key='bot')
# Set a default model
if "vertexai_model" not in st.session_state:
st.session_state["vertexai_model"] = "chat-bison"
# Initialize chat history
if "messages" not in st.session_state:
st.session_state.messages = []
# Display chat messages from history on app rerun
for message in st.session_state.messages:
with st.chat_message(message["role"]):
st.markdown(message["content"])
# Accept user input
if human := st.chat_input("Please ask assistant"):
# Add user message to chat history
st.session_state.messages.append({"role": "user", "content": human})
# Display user message in chat message container
with st.chat_message("user"):
st.markdown(human)
# Display assistant response in chat message container
with st.chat_message("assistant"):
message_placeholder = st.empty()
with st.spinner("Processing..."):
#full_response = gen_response(human)
full_response = chain(human)
try :
message_placeholder.markdown(full_response["response"])
st.session_state.messages.append({"role": "assistant", "content": full_response["response"]})
print(full_response)
#print()
except:
print("error")
実行結果
デプロイ方法は以下の記載と同じなので、ここでは割愛します。
WEBアプリをクラウドでデプロイ(Cloud Run + Streamlit or Flask) - まるっとワーク
実行結果として、会話が正常に行え、その記録もしっかり残せています。
streamlitは、変数保持に対応が必要なので、会話履歴に対しては保持するための対応をしています。
【Streamlit】Session Stateで変数の値を保持する方法 #Python - Qiita
pdfの内容に応じて答えを出してくれるアプリ
同様にLangChainのConversationChainの機能を使用しています。
ただし、特定の命令(プロンプト)を与えています。
以下はapp.pyのコードの抜粋です。
構成詳細
import streamlit as st
from streamlit_lottie import st_lottie
from langchain_google_genai import ChatGoogleGenerativeAI
from langchain import PromptTemplate
from langchain.cache import InMemoryCache
from langchain.chains import ConversationChain
from langchain.memory import ConversationBufferMemory
from langchain.text_splitter import CharacterTextSplitter
from langchain.agents import AgentType, AgentExecutor, ZeroShotAgent, Tool, initialize_agent, load_tools
import requests
from langchain.tools import WriteFileTool
import PyPDF2
import io
GOOGLE_API_KEY = "自身で取得したAPI KEYを入力"
langchainllm_cache = InMemoryCache()
llm = ChatGoogleGenerativeAI(model="gemini-pro",
temperature=0.3, convert_system_message_to_human=True,google_api_key=GOOGLE_API_KEY)
def get_state():
if "state" not in st.session_state:
st.session_state.state = {"memory": ConversationBufferMemory(return_messages=True, k=5)}
st.session_state.state["count"] = 0
return st.session_state.state
state = get_state()
print(state)
tools = load_tools(
[],
llm=llm
)
tools.append(WriteFileTool())
chain = ConversationChain(
llm=llm,
memory=state['memory']
)
if state["count"] >= 0:
prompt = PromptTemplate(
input_variables=["system_input", "document_input", "user_input"],
template="""System Prompt Here: {system_input}
Document Input: {document_input}
User Prompt: {user_input}"""
)
else:
prompt = PromptTemplate(
input_variables=["user_input"],
template="""
User Prompt: {user_input}"""
)
print("Not First")
system_input = """####Document Input#####の内容を踏まえて、####User Prompt####の命令に従って回答してください。これを厳守してください"""
agent = initialize_agent(
tools,
llm,
memory=state["memory"],
agent=AgentType.STRUCTURED_CHAT_ZERO_SHOT_REACT_DESCRIPTION,
verbose=True
)
def load_lottieurl(url:str):
r = requests.get(url)
url_json = dict()
if r.status_code == 200:
url_json = r.json()
return url_json
else:
None
def get_pdf_text():
st.markdown('Managed by: <a href="https://dango-study.hatenablog.jp/">Kazuma Tokuda</a>',unsafe_allow_html=True)
st.markdown('')
st.title(":violet[Document AI Search]")
uploaded_file = st.file_uploader(
label='Upload your PDF here😇',
type='pdf'
)
if uploaded_file:
# ファイルをメモリに読み込む
file_buffer = io.BytesIO(uploaded_file.getvalue())
# PyPDF2を使用してPDFを読み込む
pdf_reader = PyPDF2.PdfReader(file_buffer)
text = ''
for page in range(len(pdf_reader.pages)):
text += pdf_reader.pages[page].extract_text() + '\n'
text_splitter = CharacterTextSplitter(
separator = "\n\n",
chunk_size = 100,
chunk_overlap = 0,
length_function = len,
)
text_list = text_splitter.split_text(text)
document_list = text_splitter.create_documents([text])
st.session_state.pdf_text = text_list
st.write(text_list)
def page_ask_my_pdf():
load_bot = load_lottieurl("https://lottie.host/dffb1e31-78af-4548-9e7c-30fd1cbbb704/lUvwHha1IZ.json")
col1,col2 = st.columns(2)
with col1:
st.markdown('')
st.title(":violet[Document AI Search]")
if "pdf_text" in st.session_state:
pdf_text = st.session_state.pdf_text
# PDFテキストを使用して何か処理を行う
# 例: st.write(pdf_text)
with col2:
st_lottie(load_bot,height=200,width=200,speed=1,loop=True,quality='high',key='bot')
# Set a default model
if "vertexai_model" not in st.session_state:
st.session_state["vertexai_model"] = "chat-bison"
# Initialize chat history
if "messages" not in st.session_state:
st.session_state.messages = []
# Display chat messages from history on app rerun
for message in st.session_state.messages:
with st.chat_message(message["role"]):
st.markdown(message["content"])
# Accept user input
if human := st.chat_input("Please ask assistant"):
# Add user message to chat history
st.session_state.messages.append({"role": "user", "content": human})
# Display user message in chat message container
with st.chat_message("user"):
st.markdown(human)
# Display assistant response in chat message container
with st.chat_message("assistant"):
message_placeholder = st.empty()
with st.spinner("Processing..."):
custom_prompt = prompt.format(system_input=system_input, document_input= pdf_text,user_input=human)
print(custom_prompt)
print(state["memory"])
full_response = agent(custom_prompt)
state["count"] += 1
try :
#print("full_response", full_response)
message_placeholder.markdown(full_response["output"])
st.session_state.messages.append({"role": "assistant", "content": full_response["output"]})
#print("st.session_state", st.session_state)
except Exception as e:
st.error(f"An error occurred: {str(e)}")
print(e)
else:
st.markdown("まずpdfファイルを読み込んでください")
def main():
selection = st.sidebar.radio("Go to", ["PDF Upload", "Ask My PDF(s)"])
if selection == "PDF Upload":
get_pdf_text()
elif selection == "Ask My PDF(s)":
page_ask_my_pdf()
if __name__ == '__main__':
main()
実行結果
pdfを読み込むページと会話をするページを分けています。
pdfを読み込むと読み込んだ結果が表示されます。
会話をするページでは、聞いた内容及びpdfの内容も踏まえて回答してくれています。
ただ、まだ制御が怪しくきれいに出すことができていません・・
また、プロンプトインジェクションにも弱く、なかなか難しいですね・・
